熱回路網モデルは，熱容量を持つ節点と一般化熱コンダクタンスから構成される回路網で図形化され，温度の変化を表す連立常微分方程式で数式化されます．換気回路網モデルは，ゾーンの静圧の節点と流路から構成されます．
　太陽熱利用の例では，屋根面の空気式集熱器による温風を床下に吹き出して床暖房しました．
　NETSは蒸発冷却も計算できますので，屋上緑化や屋根散水も研究しました．緑化の場合は濡れ面積率を仮定します．クールチューブでは，チューブ内の結露が検討課題になりました．
　放射暖房では，PMVが0になるように，循環温水への加熱をPID制御します．ただしNETSの通常の空調熱負荷計算では，空調時間には設定の温湿度にしますが，それ以外の時や空調能力を超えた時には自然な室温変化になります．従って熱負荷計算の場合には，加熱と冷却の最大容量も与えます．
　NETSは，例えば内外温度差によって窓の開閉を模擬できます．一般的には，計算モデルの構造や係数の変化を，スケジュールあるいは状態によるフィードバック制御によって行うことが可能であり，これをモード変化と呼んでいます．

　熱回路網のシステム同定計算プログラムSPIDは，多数ゾーン間でのガス移動系にも適用することができます．両者の測定の単位系は異なりますが，数学モデルは同じだからです．熱とガスのどちらの系でも，各ゾーンへ間欠的な発熱またはガス発生の励振を与え，室の温度またはガス濃度の変化の測定データを得ます．
　実際の伝熱系の熱容量は，室空気よりは壁体等に多く含まれますが，システム同定モデルには壁体の熱容量の節点は無いので，室空気の節点に含めなければなりません．このために全ての測定値に8時間の移動平均を二重に施すローパスフィルターが良いシステム同定結果をもたらすことが分かりました．
　またゾーン間またはゾーンと外気の間には空気移動による非対称な熱移動があるので，ゾーン間の対称な熱貫流と分けて，システム同定しなければなりません．
　ここ数年の研究で，これらの条件式を最小二乗法への寄与式とすることで，それが可能になりました．さらに灯油暖房器を用いれば，十分に大きな発熱量とCO2発生も利用できて，同時に両系のシステム同定が可能になりました．

　この研究の初期では，複数の人体伝熱モデルを含む冷暖房システムを状態空間方程式で表し，最適レギュレータ制御則の計算式はラグランジェ乗数法により導き，計算機シミュレーション実験は成功しました．
　しかし現状は簡単な制御で間に合っており，こうした複雑で難しい制御を行うメリットはあまりありませんでした．
　そこで最適設計に生かす方法が考えられました．複数の人体伝熱モデルと冷暖房装置を持つ系において，制御の評価関数を，熱的快適性，省エネ性と低質エネルギー性の二次形式で表しました．状態空間方程式を定常状態に簡単化し，未知数の温湿度を解く式に変形して，その評価関数に代入しました．この評価関数を操作変数のベクトルで微分し，操作変数と状態変数を解ける式を導きました^[34][40]．しかしこれ以後の発展は止まっています．

　NETSのFORTRANプログラムの開発は，早稲田大学の修論研究^[1]で太陽熱集熱器のモデル化法を考案したことから，1975年から始まりました．当時はメインフレームコンピュータが用いられ，計算プログラムもモデルのデータも，カードに穿孔してフィードしました．まず熱回路網モデル図は紙に描き，その一般化熱コンダクタンスc(i,j)の値と節点番号iとｊ等を沢山のカードに打ち込んでいました．
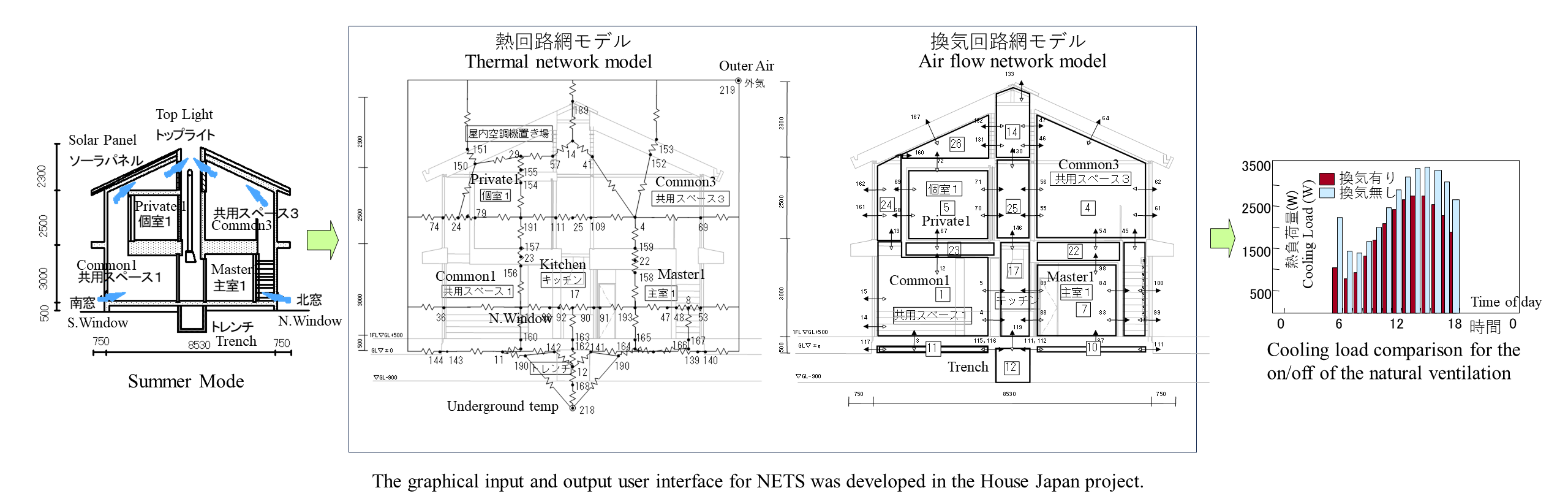
　パソコンが進化してFORTRANが走るようになり，モデルの図もデータもグラフィカルに作成可能となりました．そして1994年から始まった，ハウスジャパンと呼ばれる国家プロジェクトに参加することで，そのようなユーザーインターフェイスの開発をする機会が得られました．
　　もしも型にはまった伝熱構造のモデルしか扱わないのであれば，表計算ソフトによる入力でも十分でしょう．しかし今まで無かった様々な構造のモデルを作る必要があるので，グラフィカルで柔軟なモデル作成インターフェイスが必要です．特に，実務に適用する段階よりも，研究段階においてはそう言えると思います．

　NETSのデータ処理は3ステップとして，前処理プログラムNETSGENと，後処理プログラムNETSOUTの画面の様子を示しています．
　例えば，NETSGENでは有限要素法で柱と壁の部品モデルを作ることができます．予め部品を作っておいて，全体モデル構築で利用できます．
　空間的な離散化は有限体積法を用いることが多いのです．この熱回路網の節点方程式は様々な離散化方法のプラットホームであり，建物のそれぞれの部分で，異なる離散化法を用いても，全体の状態空間方程式が構成されます．
　最背面の画面はガラスの透過・反射の入射角余弦に依存する特性を作っている様子です．
　NETSOUTは，モデル図の上に，ある時刻での各節点の温度を表示できます．また，この図にはありませんが，温度の時間変化のグラフも表示できます．

　Pre-processor NETSGEN：熱，換気，ガスの回路網モデルを，画面上に自由に描いて構築できます．熱回路網は，節点を配置し，熱容量を与え，一般化熱コンダクタンスで節点をつなぎます．
　水蒸気もガスとして扱えます． 水蒸気などの回路網は熱回路網と同様に構築します．換気回路網は，ゾーンを配置し，外気も含めたゾーン間を，流路でつないでいきます．流路は，圧力損失係数，べき乗の指数と開口面積によるべき乗則で表されます．流路の高さとゾーンの底面の高さも与えます．
　壁などの熱回路網モデルは，予め壁の部品を作成してライブラリィに登録し，全体のモデルの構築をしやすくします．例えば，壁の法線方向を細かく分割して，節点が多すぎる場合は，最少で両表面の２節点まで数学的にコンデンスすることができます．
　最後に，熱，換気，ガスの節点の間の対応付けをします．また，ドライビング条件と呼んでいる，モデルを動かしていく条件設定を行います．
　気象データは，SHASEJの1時間毎で1年間の標準気象データの他に，ユーザーが測定して生成したデータも使用できます．非定常の計算時間間隔Δtは，1秒から1時間までで，1時間との公約数です．定常状態の計算は，節点の容量を0にすることで行われます．

　Post-processor NETSOUT：NETSOUTはNETSのシミュレーション結果を画面に表示し，データファイルを出力します．温・湿度は，モデル図の節点の傍に表示されます．これを空間分布表示と呼んでいます．また時間変化のグラフを見ることができます．さらに表計算ソフトによるグラフ作成等のために，結果をCSVファイルで出せます．
　NETSはモデルの構造的な変化を，スケジュールあるいはフィードバック制御で実施できます．例えば内外温度差によって窓を開閉する等が具体例です．
　これを一般的にモード変化の制御と呼ぶ方法で計算します．予めユーザーは，モード変化に関連するモデル要素を，番号付けした部分集合で定義し，さらにこの部分集合におけるモードの種類を番号で定義します．
　次にモード番号を操作量とするフィードバック制御則と一日における実行期間の定義をします．シミュレーションの結果として，時々刻々の各部分集合のモード番号の表も出力します．

　煙突効果は，高層の建物で大きくなりますが，仕組みを説明するのは複雑なので，上の中央の図の様に建物内部を一つの空間に単純化します．冬に屋内が暖かく，外気が寒いとしますと，屋内と屋外の高さ方向の圧力の関係は，右上のグラフの様になります．
　外気は比較的に低温で密度が大きいですから，高さ方向の圧力の減少も大きく，傾きも大きくなります．しかし屋内は比較的に高温ですから，密度が小さく，傾きが小さくなります．そして内外の圧力差が生じます．この圧力差がゼロになる高さを中性帯と呼びます．建物の上下方向で外壁の開口や隙間が大きい方に中性帯は移動します．
　外皮の隙間や開口では，下の方は外気が入り込み，上の方は屋内の空気が出ていきます．
　住宅のような多数室間でも，隣り合う室間に温度差があれば，煙突効果により，室間の開口の上下で逆方向の流れが生じることがあります．
　換気回路網の計算モデルにおける流路のモデルは，1方向の流れしか表現できません．そこで開口や隙間の上下には少なくとも2本の流路を仮定し，両方向の流れが模擬できるようにします．

　例えば，ダブルスキンのグレージングで起こる温室効果と自然排熱を述べます．日射はガラスを透過して室内に入って床などに吸収されます．床の温度は上がり，長波長放射をしますが，ガラスを透過して外へ逃げられません．ガラスは光のような短波長の放射は透過させやすく，長波長の放射は透し難いからです．太陽エネルギーは室内に捕らえられ，温室効果が生じます．冷房負荷も大きくなります．
　そこでダブルスキンの通気層の中にブラインドを垂らして，ブラインドが吸収した熱は，煙突効果により自然に外気に排気する等の対策が行われています．
　NETSでは，直達日射に関して，入射角度θ 依存の，透過率と反射率を，入射角余弦COSθの５次の冪級数の回帰式で計算します．この回帰式の係数は，予め最小二乗法で求めておき，ライブラリィに保存しておいて利用します．
　また，ブラインドの計算モデルでは，入射角度ではなく，プロファイル角を用います．

　時々，通気層を利用して，日射熱を利用したり，逆に日射熱を排熱したり，等の提案が見られます．そこで通気層の熱的な効果が過大視されていないかという疑問が持ち上がります．
　また室内側にも通気層を設けるのは正しいのかという疑問もあります．熱的な効用よりは，水蒸気排出の効果が重要と思われます．壁の内部結露が起これば，建物の耐久性も低下しますし，カビなどが生えれば居住者の健康にも良くないです．
　また，通気層が壁の下方から屋根の上方まで長くつながっているのは正しいのか，さらに風圧に対する等圧区画が無くてもよいのかという疑問もあります．
　2017年にロンドンの高層の集合住宅で火災事故がありました．外壁の断熱材が通気層に沿って燃えて上方に広がりました．従って，壁の通気層が高さ方向に長くつながっているのは，良くないと考えられます．あの場合は，断熱材は可燃性の発泡プラスチックでした．また通気層内に等圧区画を設けないと，風圧により雨水が侵入しやすくなります．
　この例では様々な適用の仕方の通気層を研究するために，断熱材の外側と内側の両方に通気層を設けておき，通気層にはダンパも設けたモデルにしました．

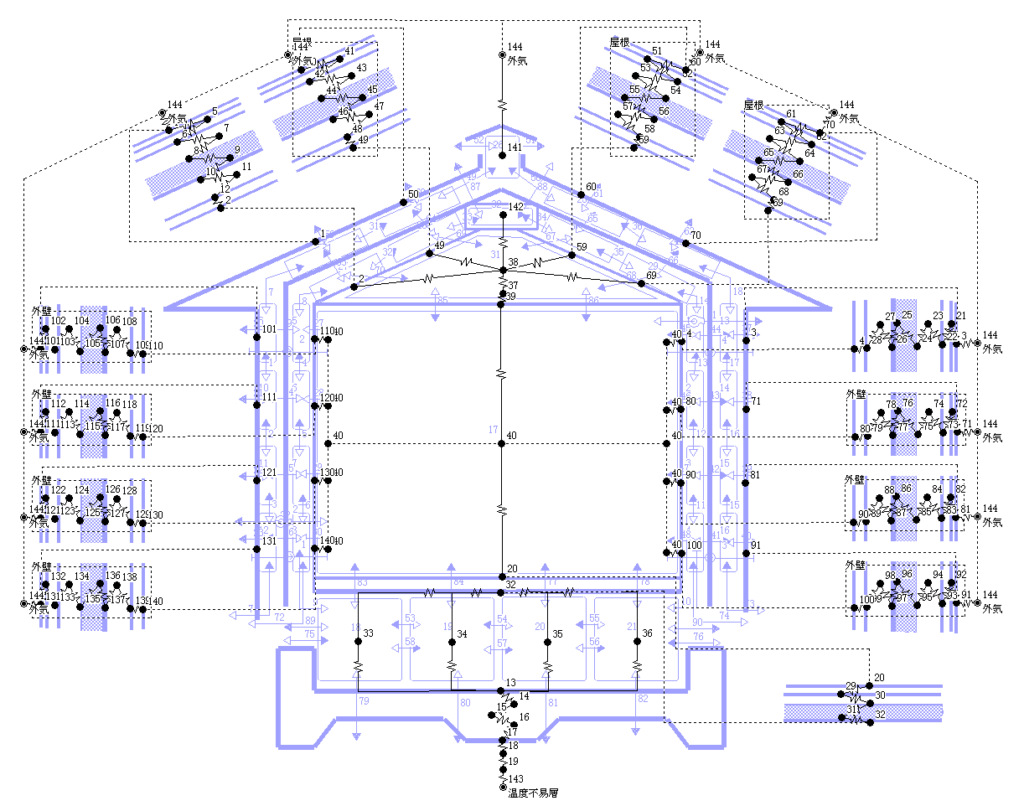
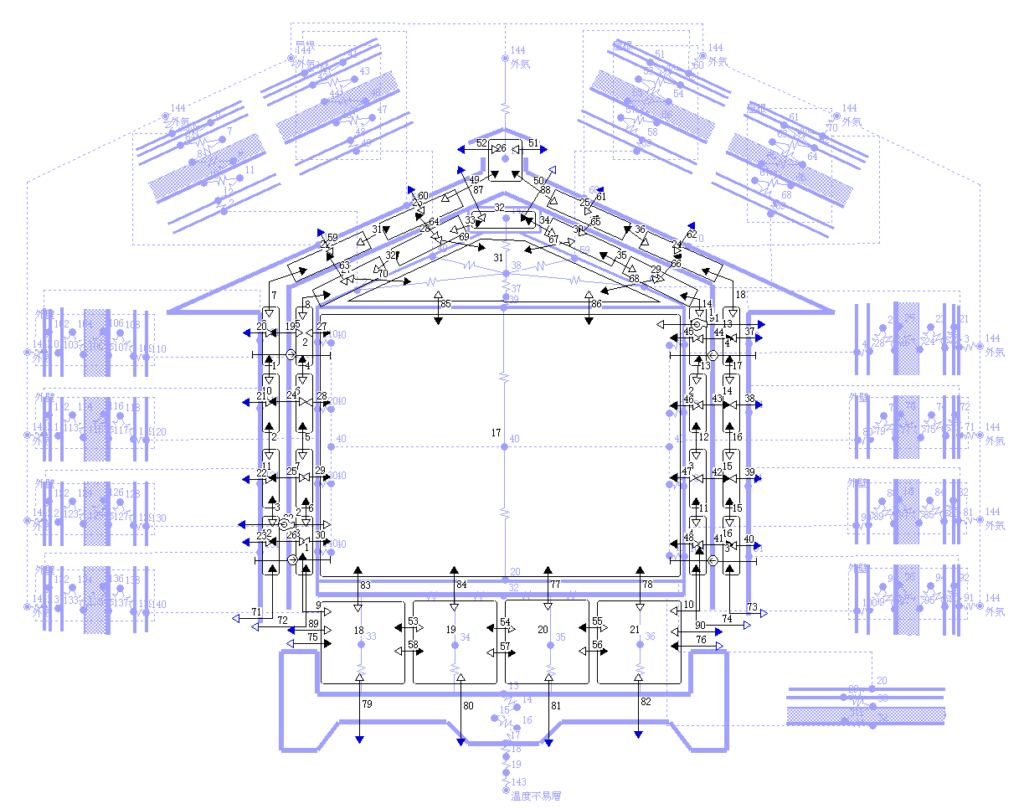
　換気回路網モデルの図を描く際に，この下に敷いた半透明で薄い青色の熱回路網モデルをガイドにします．
　通気層内の空気の流れ方向は，幾つかのゾーンに分割して，温度変化と絶対湿度の変化を模擬します．分割しない1分割よりは近似度が良くなります．
　実態より高気密な換気回路網モデルでは，送風機による室内の加圧あるいは減圧により，それぞれ実態よりも大きな高圧あるいは低圧の計算結果になります．そこで実現象に近い室内圧が解かれるためには，隙間のモデルが重要です．ここでは多くの実測から，経験的に得られている相当隙間面積を外壁の全体に均等に配分しました．
　ただし現状の隙間の計算モデルは，べき乗則の指数は２と仮定して定められているので問題があります．今後は，二次式モデルを導入し，相当隙間面積だけでなく，物理学的に意味のある，隙間の深さと幅の比率等の係数も用いるべきと思われます．
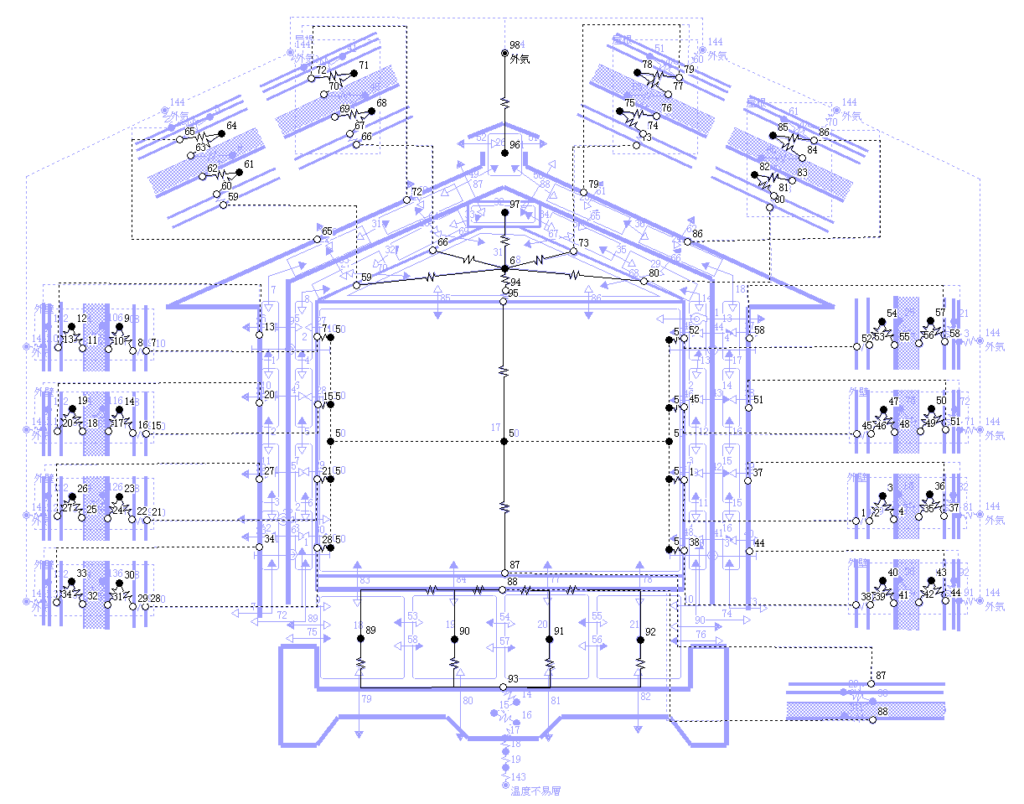
　伝熱，換気と水蒸気移動のモデル作成の次に，各系の節点間の対応のデータを作ります．そしてゾーンの空気密度が計算され，部材表面での相対湿度も計算される様にします．

　熱と水蒸気の移動が連成した回路網モデルの数学モデルと解法[7][8]，さらに水蒸気吸着率κと水蒸気放出率νの定め方[81]も研究しました．ただし，この計算モデルでは，水蒸気の伝導は簡便に定常状態を仮定しました．水蒸気の移動は隙間風によるものが大部分になります．
　モデル図において，壁の中の詳細を全体図の中に描くのは難しいので，この部分を拡大した図を，そばの別のところに描けば，分かり易くなります．全体図には壁の両表面の節点だけ描きます．これらの両表面節点の番号付けは，詳細拡大モデルのものと全体モデルのものは同じ番号になります．
　また，熱，換気，水蒸気の３つのモデルの節点の対応付けを行います．水蒸気回路網では，絶対湿度の連立方程式が解かれますので，対応する温度から相対湿度も算出されます．

　左の上下二つのグラフは，夏季と冬季の一週間における日積算の冷房負荷と暖房負荷になります．右のグラフは，冬季2月8日の一日を例にとり，壁内の断熱材について，外側の表面の相対湿度を表します．
　冷房負荷は，外側の通気層を閉じた場合に比べて，開いて流すことにより，10%減少するようです．通気層の幅が非常に大きいこと，壁と屋根の通気層をつないだこと等により，日射排熱効果が大きくなったと思われます．
　暖房負荷は，外側も内側の通気層も，閉じた方が開けた場合に比べて約25％少なくなります．しかし右のグラフの内部結露の検討結果から，外側の通気層を閉じますと結露を起こしてしまいます．ここに示した以外の計算モデルの条件でも沢山の計算をしました．
　内部結露防止に外側の通気層は重要な働きをします．水蒸気排出に必要な風量は，熱的な効果は小さい，わずかな量でも間に合います．また日射の排熱効果も少しはありますが，冬季に暖房負荷は増えるので，小さな通気量で十分です．
　なお通気層はもっと狭い0.01m程度の計算モデルで再検討すべきです．

　データセンター等では情報処理装置による内部発熱が大きいので，大きなエネルギーを消費して冷房が行われています．しかし多層階であれば，煙突効果による自然換気冷却が可能ではないかと思われます．
　しかし，ELVシャフトの竪穴により，各階の自然換気量が，大きく異なってしまうのではないか懸念されます．例えば，下層の階に入った外気が温められ，ELVシャフトを上って行き，上方の階に入れば，上方の階は十分に冷やされません．
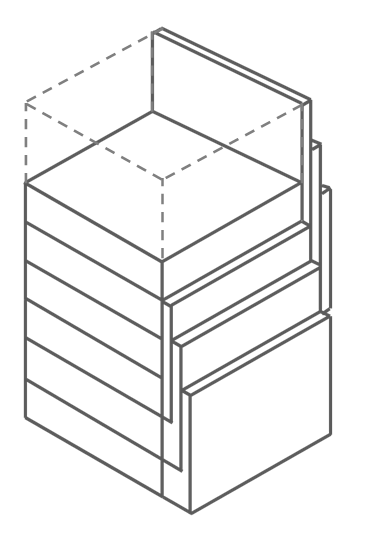
　外観のアイソメ図を示します．各階から，排熱の煙突にする扁平な矩形ダクトを三層分の高さで伸ばします．三層分のダクトは重ねます．さらに上方の三層では，ダクトを取り付ける側面を90度回していきます．このやり方を繰り返せば，何層の建物でも排熱ダクトが取り付けられます．ただし最上の三層は通常の事務所として使うことになります．
　各階の床下空間に外気が入り，グレーチング状の床から室内に吹き出し，多孔天井を通って天井裏空間に行き，そして排熱ダクトから排気されます．排熱ダクトは，ソーラーチムニー効果も利用するために，ガラスで構成します．

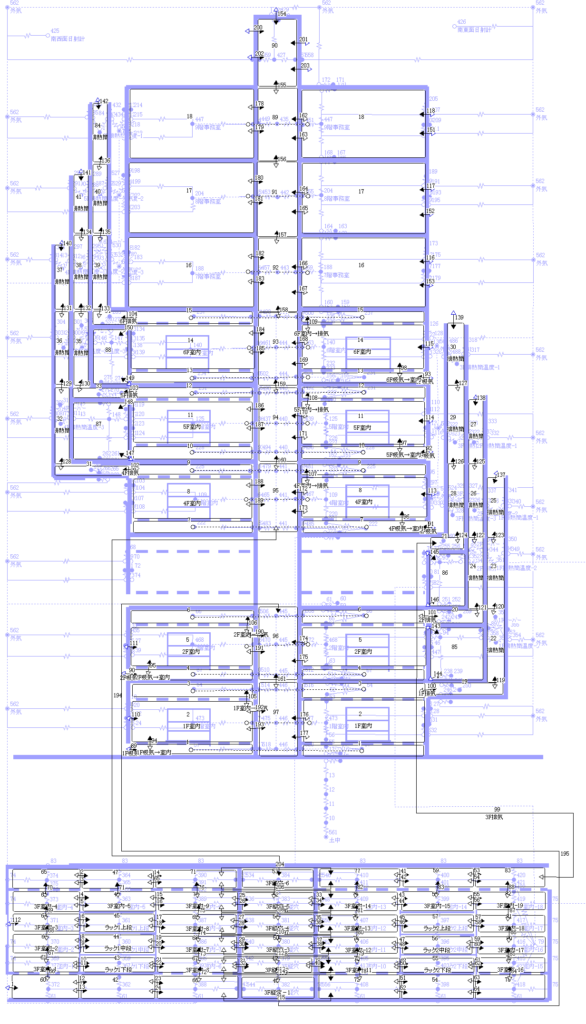
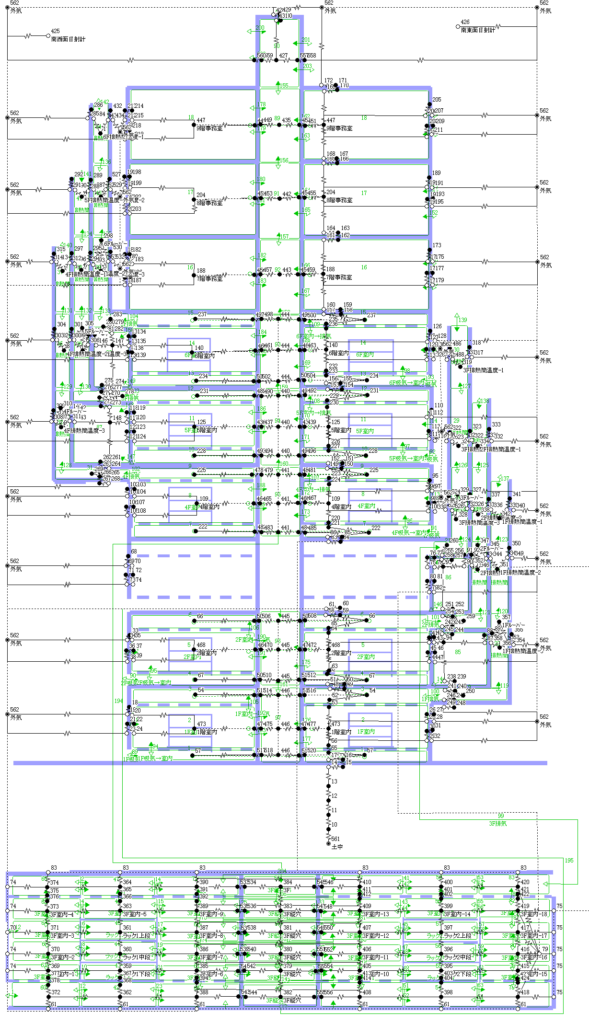
　左は換気回路網で，右は熱回路網のモデルです．壁体の熱容量も考慮しています．従いまして4日間の非定常の計算を行いまして，助走期間を3日間として，最後の1日分の計算結果を用いました，東京の標準気象データで計算しましたが，外気温度だけは0℃一定とすることで性能評価がしやすいようにしました．
　各々の建物全体的モデルの下の方には3階の詳細階を示します．将来，換気回路網のマクロモデルと数値流体解析のミクロモデルの連成をするために試みました．数値流体解析は静圧と動圧を分けたモデルですが，換気回路網は全圧を静圧としていると見なせます．本質的には正しくないのですが，3階の空間を細かく区切って，換気回路網にしてみました．
　今回の検討にはありませんが，ソーラーチムニー効果の検討も行いました．排熱ダクトのガラスを表す節点を設け，日射吸収を考慮しました．排熱ダクトの中にはブラインドが設けてあり，ガラスを透過した日射はブラインドに吸収され，温室効果が考慮されます．

　　計算結果が示されます．左上のグラフの横軸は1階から6階まで表します．縦軸は直接侵入の外気流量を，その階の容積で割った換気率になります．直接侵入には，下の階などを経由して入ってきた外気流量は含みません．
　エレベータ扉の開き程度を開口面積で表します．隙間的な状態の0.0045m2から，0.045m2，0.45m2，そして全開の４.5m2です．もし隙間的な状況の場合は，全ての階において，約50回の換気率になります．もしELV扉が全階で開いていれば，最上階の6階は換気率が毎時30回ぐらいに下がります．
　左下のグラフは，ガス濃度で評価した実効換気率を示します．下の階に入った外気流量は，途中で温められながらも，多少は冷却能力があります．そこで実効換気流量を定義します．実効換気流量は各階でトレーサガスを発生した場合の各階のガス濃度から計算できます．この実効換気率は，不利な最上階でも毎時40回ぐらいになります．右上のグラフは，外気温が0℃として，各階の室温が何度になるか表しています．全ての階は4℃ぐらいになる結果になりました．もし換気しなければ30℃ぐらいになりますから，大きな冷却効果だと思われます．

　ここに，室の一面の壁が200mmのグラスウール断熱材になっていて，換気のために，壁を通して，冬は外気を吸い込み，夏は排気する様子を描いてあります．冬は送風機で室内を減圧し，夏は加圧することで壁を透気させます．すると冷暖房熱負荷が少なくなると言われています．
　この省エネの仕組みは，定性的に説明できます．冬の減圧換気の場合は，断熱材を透過して外気が入ってきます．すると通過中に外気は温められ予熱されることになります．従って換気負荷が減ります．
　夏の場合は，冷房された空気が断熱材を通ることによって内表温度は室温に近づきます．従って内表面伝達による熱負荷が減ります．
　同じダイナミック・インシュレーションという呼び名で，二重ガラスの通気窓について研究されています．この仕組みも同様に考えることができます．これは冬季の内部結露防止に行われる場合もあります．

　熱負荷計算は，様々な換気の流量での計算モデルを，例えば4行4列で16個のモデルを画面上に並べて描き，沢山の条件の計算結果が一度で得られるようにしました．
　断熱材の厚み方向の状態値の変化を5分割して近似しました．換気モデルも5ゾーン設けました．其々のゾーンには温度と絶対湿度の節点が対応します．一般化湿気コンダクタンスは空気移動による割合が大きくなります．
　結果のグラフは，横軸に通過気流速のミリメータ/毎秒をとりました．縦軸には，透気させない場合の熱負荷に対する比率を熱負荷低減比率としてとりました．
　加圧換気と減圧換気の曲線は，殆ど同じ曲線になりました．そして最小の熱負荷にする，通過気流速度の最適値は約0.2mm/sとなりました．
　省エネの仕組みは両者で異なるのに，どうして同じ省エネ効果なのかは，もっと大局的な原理から説明できるかもしれません．

　炎天下に駐車中の状況では，車内が外気温度よりもはるかに高い温度になるのは温室効果によります．そして時々，子供を車内に置き去りにしたことで悲惨な事故が起きています．これは温室効果が多くの人にはなかなか理解し難いことを示しています．
　また，足元と頭部の温度変化を測定すれば，約半時間で大きな上下温度差が生じることが分かります．この現象もまた分かり難いと思われます．日射がガラス窓を透過して車内の何かの表面に吸収されれば高温になって上昇流を発生します．一方で，日射が当たらない室内表面は比較的に低温なので下降流を起こします．この結果，温度成層化という現象が生じます．
　こうした現象の予測計算には数値流体解析が必要であると思われていますが，長時間の非定常の予測計算には向いていないようです．そこでこの現象を近似的に計算できる熱と空気の移動の回路網モデルを工夫して可能性を研究しました．

　温度成層化の熱移動回路網と空気移動回路網のモデル図を我々は描くことができます．車内の空間は三種の領域に分けられます．上下方向を4層に分けた温度成層化の領域，日射により加熱された表面で生じる上昇流の熱プルーム，さらに外気温により冷却された表面で生じる下降流の温度境界層の領域です．
　熱プルームの上昇流は温度成層化領域の最上部のゾーンに流れ込みます．熱プルームは室内表面だけでなく，発熱体の位置によっては室空間の中央付近でも立ち昇る場合もあり得ます．一方，下降流の温度境界層からは温度成層化ゾーンの最下部に空気は流れ込みます．
　これらの流れは密度流とも呼ぶことができます．NETSでは空気密度ρ(kg/m3)は絶対温度をT(K)とした場合にρ=353.2/Tで計算します．
　エアコンなどの強制対流の装置が稼働した時には温度成層化ゾーンの間の混合流が大きくなって車内温度は一様に近づくと考えます．

　上半分には熱移動回路網，下半分には空気移動回路網のモデル図を示します．下半分の空気移動回路網はゾーンとフローパスで表すので，温度成層化モデルに近い形になります．熱プルーム内の温度節点には日射受熱をする節点をつなげます．日射を受けないので熱くならない内表面節点は温度境界層の節点につなげます．外皮には構造上のリブなどがありますから熱橋としての影響もあります．一般部分に対する熱橋部分の熱コンダクタンスの割合が実験値に合うように調整しました．さらに温度成層化ゾーン間の圧力損失係数ζと，層間の混合流による一般化熱コンダクタンスci,jの２つの係数の最適値を求める必要がありました．そこで足部と頭部の両方の温度について，予測計算温度が実験測定温度に近くなる様に決めました．このための評価関数として，これらの温度差の実験期間での積分値をとりました．そして最適の２つの係数は探索法によって求めました．これらは，ci,j=3.5 (W/K)，ζ=12 となりました^[85]．従って本工学モデルは，回路網モデルの構造は妥当かもしれませんが，係数の与え方に今後の課題を残します．

　左上は温度成層化の仕組みを表すモデル図です．熱プルームの上昇流，温度境界層の冷却下降流，温度成層化の複数ゾーン層から成ります．
　３つの時間変化のグラフは実験値とNETSによる予測計算値の比較です．右上のグラフは2005年7月29日に横須賀で行われた屋外実験です．快晴の日射量と外気温の朝の9時21分から11時25分まで約2時間の自然な車内温度の推移を調べました．この時間帯の平均の水平面全日射量は約900[W/m2]でした．
　また環境実験室のグラフは下の２つです．日射発熱を模擬して車内に電熱発熱シートを貼り発熱させています．強制対流の場合は車内に攪拌ファンを置きました．
　自然対流加熱の場合は，攪拌ファンは使用していないので上下温度差が大きくなります．
　実験値と計算値は良く一致していますが，これらの実験値に一致する様に，循環流の圧力損失係数と，温度成層間の混合流による熱コンダクタンスを調整したわけです．
　従いまして，これらのモデルの係数について，例え経験則的な方法であっても，より一般的な適用性を持つ決定方法が必要と思われます．

　熱回収の二重ダクトとは，比較的に小さい直径d1のスパイラルダクトを大きい直径d2のスパイラルダクトの中に入れた，二重のダクトから成ります．内側のダクトは外気の取り込みに使い，外側のダクトとの間は排気に使います．
　主に集合住宅で使うことを想定しました．集合住宅では，浴室とトイレに他の部屋からの空気を集めて，ダクトで排気します．潜熱回収により水蒸気や臭いが屋内に戻って来てしまうのはよくありません．この検討例では，浴室からは24時間排気し，小さな厨房からは朝と夕方の2回1時間ずつ排気するものとしました．
　ダクトの中の温度変化は流れ方向を数分割してモデル化します．解析的な温度変化の解式は導きましたが^[131]，ダクト周囲の空間と熱的な相互影響があるので本件には適用できません．
　仮に十分な熱交換面積があった場合に，出口温度が到達する究極温度θ_∞が計算できますから，熱回収効率の評価にはこれを基にして利用できます．数式は最後のスライドに示します．

　ここに換気回路網モデルを説明します．ダクト内の温度変化を模擬するためにダクト長さを４分割から７分割しました．ダクトからの漏れを考慮し，給・排気の送風機は出口側に設け，第一種換気としました．ただし実際に送風機をダクトに取り付ける仕組みは今後の課題です．
　異常な室内圧にならないように，相当隙間面積は，多くの実測値から経験的に知られている1cm²/m²と仮定し，これを外皮に均等に隙間のフローパスを分散して配置しました．
　小型厨房のフードの捕集効率を模擬するためにコンロの上に捕集ゾーンを仮定しました．捕集ゾーンは周囲の空気よりも温度が高いので上部では周囲に流出して下部では周囲から流入しますが機械排気により低い圧力になれば上部でも流出はしなくなり捕集効率は高くなります．
　近年は深さが浅い排気フードが好まれていますが煙突効果利用は期待できません．しかしフードの四辺に狭いスリット状の吸い込み口を設け風速を大きくし静圧を低くすることで吸引効果を高めています．換気回路網でこの現象はモデル化し難いかもしれません．

　ここに熱回路網モデルについて説明します．スパイラルダクトの内・外表面にそれぞれ節点を設けました．鋼板の厚みは0.5mmと仮定しました．全体のモデル図では分かり難いと思われますので，ダクトの断面を拡大した図を描き加えました．
　鋼板の両表面の節点は比較的に熱容量が小さいので省略して熱貫流率のコンダクタンスでモデル化することも可能です．しかし両表面の結露の計算のためには水蒸気の節点が必要なので，これらに対応する熱回路網の節点も必要になります．
　一般に，伝熱系と換気系の連成計算を行う場合には計算時間間隔⊿tは短めにしなければなりません．伝熱系では空気の温度が解かれ，そして空気の密度が計算されます．これらは換気系の駆動条件になります．換気系で解かれた流量は一般化熱コンダクタンスとして伝熱系を構成します．これらの相互影響は⊿tの時間遅れがあります．本件では⊿t=5分としました．
　もし上下左右の隣住戸の室温も解くとすれば，さらに大きな計算モデルが必要になります．そこで隣住戸の室温は，よく熱負荷計算で行われる外気温度比率の考え方で仮定しました．

　水蒸気移動回路網モデルを説明します．結露が懸念される場所は，多めの水蒸気を含んだ室内空気が外に排気され，低い温度の外気が吸い込まれる吸・排気口の付近です．しかし例え結露しても，水は外気に吐き出され室内に入ってこない場所なので大きな問題にはならないと思われます．
　例えばダイナミック・インシュレーションにおいて，グラスウールの断熱材を通して冬季の暖房加湿した室内空気を外気に排気した場合に，外気側の表面で結露が起こるという話は聞いたことがありません．ただし実験して確かめる必要がありそうです．
　ダクトの鉄板は水蒸気を通しませんので，ダクトの内・外表面の二つの節点の間は切断しています．水蒸気移動は空気移動によるものだけとし，壁体等の湿気伝導は省きました．
　水蒸気発生は，浴室洗面室の常時発生，間欠的な寝室の人体発生と台所の発生を与えました．

　このケーススタディをしたホステルが福岡にありますので標準気象データは福岡の1月の2週間を用いました．室内は22℃一定で換気の熱負荷を計算しました．
　比較した条件は ‘no heat recovery’ の場合，二重ダクト長さを1.8mから3.6mにした ‘double heat recovery area’ の場合，1.8mの ‘standard heat recovery area’ の場合，二重ダクトの外側に断熱材を巻かない ‘no insulation’ の4通りです．
　熱回収しない場合に比べて20％ぐらいの省エネになるようです．先ほどの究極出口温度を基準して定義した熱回収率ηは約0.4になりました．仮にダクトが2倍の長さであれば，約0.65になります．さらに断熱材で巻かない方が導入外気が温められて熱回収率は良くなります．外気取り込み温度は，内外温度差の半分程になり，冷風感の緩和は期待できると思います．無断熱建築なので外壁の貫流熱負荷が大部分を占めます．換気量は毎時約1回であり換気負荷は比較的に小さいです．従って暖房負荷全体における換気熱負荷の低減効果はわずかです．

　人工気候室を持つ住宅会社もあります．それは二階建ての戸建て住宅が入いるぐらいの大きな空間であり，空調装置と人口太陽灯と降雨装置等により，寒冷や酷暑の外界条件を何日間も一定につくることができます．そして住宅の中を電熱ヒータで加熱して撹拌機で一様な温度にして達した一定温度から住宅全体の熱貫流係数は簡単な計算で求められます．この方法は性能評価はしやすいのですが実施費用が大きいと思われます．
　一方，実態の建物では断熱性や気密性の経年劣化があるかもしれませんし，施工ミスがあるかもしれません．従って実態の建物で現場測定する方法が必要と思われます．しかし，変動する外気温や日射量等の気象条件に曝されるので性能評価は簡単ではありません．さらに実態の多数室的な状況での室間の熱貫流係数を推定する必要もあります．

■1983年:熱回路網のシステム同定理論を考案しました[10],[13]．
■1985年:日本原子力研究所･保健物理部からの受託研究で，第一世代の多数室換気測定システムを試作しました[17]．
■1987年:多数室換気測定法の検証実験をスウェーデン国立建築研究所で行い，Pergamon Press社のB&Eに発表しました[26] ．
■1991年:第二世代の測定システムを試作し，電力会社や住宅会社等の受託研究で，幾つかの住宅で測定を実施しました[31],[35]．
■1997年～2002年:国際会議で発表[47]. 筑波の建築研究所のシリンダーハウスで多数室換気測定法の検証実験を実施しました[50],[51],[65]．
■2007年～2009年:多種PFTによる多数室換気測定の統計的データ分析法も考案しました[84],[86],[87]．
■2012年:我々はElsevier社のB&Eに，改良されたシステム同定理論[99]，Airtightnessの測定法[97]，トレーサーガス濃度減衰法[98]を発表しました．
■2019年:国からの研究補助により第三世代の多数室の熱・換気測定システムを試作しまして，幾つかの住宅会社で測定を実施しました[124],[125]．
■2021年:実用性向上を目指し，複数の灯油暖房器を利用した換気と熱性能の同時測定法を考案しました[136],[139]．
■2022年:福岡のホステルで測定実験しましたが，準備不足により発熱量が不足で残念ながら失敗しました[141]．
　そこでこの再実験の機会を期待し再挑戦したいと思います．

　科研費の補助で第三世代の多数室換気測定システムを試作することができました．また動作確認実験について紹介します[125]．　
　測定システムは次の様な装置から構成されます．各室の炭酸ガス濃度と温度と湿度を測定する箱．各種の制御と測定と記録用のラップトップパソコンが2台．炭酸ガスボンベが2本．ガスを各室へ分配する2箱．そして各室内の空気の攪拌機などです．なおこの測定システムは最大で9室に対応できます．
　動作確認実験を行ったのは，横浜の集合住宅の4階にある3LDKの住戸です．2019年の4月22日に約5時間の測定を行いました．システム同定は7室のモデルとしました．リビングでのガス供給とガス濃度変化のグラフを示します．ガス供給は正弦波形で15分間供給しました．最大流量は12L/毎分です．ガス濃度は最大2000ppmぐらいになりました．
　最小二乗法を用いれば，各室におけるガス供給流率の時間変化とガス濃度の時間変化と外気濃度などの測定値から，室間の空気流率と室と外気の間の空気流率および各室の有効混合容積を推定することができます．この計算処理をガス移動系のシステム同定と呼んでいます．

　多数室換気測定システムの実験結果を示します．システム同定された空気流率分布を表します．全室での換気率は1.1[1/h]です．このうち機械排気は0.92[1/h]となりますので設計換気率に近くなりました．
　左下の数表はシステム同定された有効混合容積です．幾何的な容積よりは少し小さくなりました．
　システム同定されたガス移動回路網モデルに，測定されたガス供給流率を与えて，各室のガス濃度変化を予測計算しました．右のグラフは，リビングルームについて，予測計算のガス濃度変化と測定濃度変化を比較したものです．良く一致していると考えられます．
　信頼性の評価指標の決定係数CODは0.926で妥当です．独自に定めたシステム同定の前提の不適合率βは0.958ですが，これも妥当です．ここに，βは 1 に近いほど正常で，もし大きすぎる場合には，システム同定の前提の不成立が疑われます．

　多数室熱性能測定システムの動作確認実験を示します[124]．
　測定システムを構成する機器は次の通りです．各室の電熱発熱の制御装置．発熱制御と測定と記録の2台のノートパソコン．各室の温度・湿度の測定装置．そして各室の電熱器と室空気の撹拌機などです．
　実験対象の建物は換気測定と同じ集合住宅です．4階の3LDK，竣工は2013年，床面積は66m2，屋内容積は138m3になります．測定期間は換気測定よりは早く，2018年の11月14日18:10から18日18:10までの4日間でした．
　右下のグラフは，最大容積のリビングへの加熱と室温変化になります．発熱はゆっくりした室温変化にするために正弦波形の谷から谷までは2日間にしました．最大発熱量は1.8kWで，最高の室温は35℃ぐらいになりました．

　こちらは多数室熱性能測定システムの実験結果です．実は測定法の検証としては大きな問題がありました．それは上下左右の隣住戸の室温が測定できなかったので外気温と見なした事でした．この問題はシステム同定の前提の不適合率のβが１よりも大きい値になって示されました．
　さらに，システム同定された熱回路網モデルに，測定された発熱流率と外気温を与えて予測室温変化を計算し，リビングの測定室温について比較しました．するとグラフの様に大きな違いが見られます．これらの問題から今後の課題が次の様に考えられます．
■上下左右の隣住戸内にも発熱を与え，評価対象住戸と大きく異なる室温と時間変化を生成して測定する必要があります．
■システム同定する室間と隣住戸と外気との一般化熱コンダクタンスには空気流率の分も含まれるので壁の熱貫流分と分ける必要があります．従って多数室換気測定も同時並行で行う必要があります．
■実際の住宅において電熱発熱では十分な内外温度差を生成する加熱力を持たないと思われます．従って灯油暖房器等の別の加熱装置が必要と思われます．加熱流率は灯油重量の減少速度から推算できます．

　これまで研究・開発した測定法の問題点と，現在検討中の改良法を紹介します．
　熱性能測定では，電熱ヒーターを用いますと加熱力が不足して，十分な内外温度差が得られない問題がありました．また換気測定では，ガスボンベと流量制御装置が複雑になるので，実用性に問題がありました．
　そこで灯油暖房器の燃焼を利用することにしました．その燃料の重量減少を精密な電子秤で測定することで，発生熱流と炭酸ガス発生流を推算する方法の検討を始めました．この方法により伝熱と換気の同時測定が可能になります．
　灯油暖房器は1から2日間の燃焼と停止を手動で行います．各室の室温と炭酸ガス濃度は小型測定器で1分間隔で測定記録します．

　熱やガスの移動系のバランス式と，システム同定する係数の c i,j, m i,j, r i,j について説明します．
　この(1)式は，伝熱やガス移動それぞれの節点系における熱流収支やガス流収支を表しています．変数の x は伝熱系では温度を表しますが，ガス移動系ではガス濃度を表します．変数のｇは，発生熱流やガス発生流を表します．
　この回路網モデルでは，三種類の係数があります．記号c i,jは一般化コンダクタンスと呼んでおりまして，様々な伝熱形態を表します．ガス移動系では空気流量を表します．
　m i,jは，相当熱容量や有効混合容積を表します．さらにr i,jは，伝熱系では日射熱取得係数等を表しまして，ガス移動系では単位の換算係数等を表します．こうした三種類の係数を，最小二乗法に基づくシステム同定によって推定します．

　システム同定の係数 ci,j, mi,j, r i,j を含むベクトル a の最小二乗解の概要を示します．先ほどの節点方程式(1)から，全体系の(2)の連立常微分方程式が構成されます．これは状態空間方程式とも呼ばれます．測定は時間積分間隔⊿tが1分で行われるとします．(2)式が含む各種変数を(k-1)⊿tからk⊿tまで台形近似積分することで被同定係数のベクトル a に関する(3)式の回帰式を得ます．
　測定期間は全部でnt時間ステップあるとします．全測定期間における最小二乗法により (4)式が得られます．
　一方，壁の熱貫通の一般化熱コンダクタンスの場合は ci,jと逆方向の cj,iは対称で等しく ci,j=cj,i の条件式があります．これをSとdで表して(5)の最小二乗式が得られます．さらに壁をはさんで対称の熱貫通成分と非対称の空気移動成分の両方がある場合でも，これらを分けて推定するための追加条件もこの(5)式に含められます．さらに(4)と(5)式を束ねた(6)と(7)式の回帰式が得られます．さらに最小二乗の評価式(8)から最小二乗解(9)式が得られます．

　壁を挟んで対称性を持つ熱貫通成分ui,j=uj,iと換気などにともない生じる非対称性の空気移動成分を分けて同定する方法を示しています．
　この二階建て二室の建物の熱回路網のシステム同定モデルにおきまして，１，2階の間の床の熱貫通コンダクタンスを求める場合を考えます．
　多くの場合，建物の煙突効果で1階から2階への上昇流が階段の穴などを通して生じます．2階から1階への空気流率は小さな場合が多くなります．一般化熱コンダクタンスc1,2とc2,1の構成成分である熱貫通成分と空気移動による成分をそれぞれ(10)と(11)の式で表します．(10)式から(11)式の両辺を差し引けば(12)式になります．この(12)式を最小二乗の拘束式として(5)式のマトリックスSとベクターdの中に加えます．
　空気流率qi,jとqj,iは多数室換気測定データからガス回路網のシステム同定を行っておけば与えることができます．まず非対称性の一般化熱コンダクタンスを推定し，さらに熱貫通成分のu1,2とu2,1がシステム同定されます．

　壁を通過する熱流が熱貫流だけから成るならば一般化熱コンダクタンスci,j はci,j=cj,i の対称性の拘束条件が成立しなけれなりません．ここで c の添え字の i と j の順番は熱流の方向に関係します．例えばci,jは節点 j から節点 i への方向のものです．線形代数ではマトリックスAのi行j列要素はai,jと記述する約束があります．これに一致してコンダクタンスマトリックスCのi行j列要素がci,jと記述されます．さて壁の隙間や穴を通過する空気移動による熱移動も含まれる場合は双方向の ci,jとcj,i が数式(12)で表される ci,j-cj,i=(空気流率による一定値)の非対称性の拘束条件を満たさなければなりません．さらに何れの節点でも質量流量収支が成立するのでΣci,j = Σcj,i の拘束条件が成立しなければなりません．そしてn個の全節点で必ず必要な拘束条件式です．各室で測定の温度やガス濃度の時間変化データ等による最小二乗解の(4)式の次数（連立方程式の行数）は同定係数の個数に等しくなります．一方，全部の拘束条件式からの最小二乗解の(5)式の次数（連立方程式の行数）も同定係数の個数と同じです．従って両者それぞれで一度最小二乗解式を得てから，さらに両者を連立して全体の最小二乗解の(9)式を得れば両者から最小二乗への寄与度が同程度になり合理的です．

　著者は本研究の初めのころから”熱回路網モデルのシステム同定法”と呼んでいました．しかし最初の応用はトレーサーガスの移動系に多数室換気測定法としてでした．多数室でのトレーサーガス移動系も多数室での熱移動系と同じ熱回路網の数学モデルで表されます．しかし熱移動系でも成功するためには，システム同定のための励振と呼んでいる各室への加熱の波形の工夫と時間変化する全ての測定値に施すローパスフィルターの工夫が必要でした．
　多数室熱性能測定法の計算機実験の成功は2012のB&E誌の論文に報じました[99]． 励振の波形は正弦波で，谷から谷までの1周期は3日間でした．壁のオーバーオールな熱貫流率は定常状態で定義されるので，励振もなるべくゆっくりした変化が必要と考えられました．また全ての測定値にローパスフィルタとして8時間の移動平均を施していました．
　しかし実用的な観点からは矩形の励振が使えれば便利です．そこで移動平均を2回施す方法を試したところ良い結果が得られました[139]．
　グラフで示される様に，元の矩形波形に1回の移動平均だけでは角が残りますが，2回の移動平均を施せば，丸みのある滑らかな曲線になることが分かります．

　改良した測定法の効果を計算機実験によって確かめました．計算機実験により模擬測定値を生成するための換気と伝熱の回路網モデルをスライドの左に示します．右にはシステム同定モデルとして炭酸ガス移動と熱移動のモデルを示します．これらのモデルは2012年に出版された論文の研究で用いた計算モデルを基本にしました．
　灯油燃焼がありますので，それぞれの室の換気率が毎時1回程度になるように，機械換気流率を与えました．ただし隙間を通る自然換気もわずかに加わります．熱回路網の総節点数は壁の中の節点も含めると合計63個となります．これらのモデルの他にガス濃度を計算するガス移動回路網モデルも連成していますが図は省略します．　
　一方システム同定モデルはガス移動も熱移動も２つの部屋に対応する2節点のモデルです．ガス移動回路網のシステム同定により室間の双方向の空気流率を求め，これらは熱移動のシステム同定での最小二乗法への寄与式になります．そして空気流以外で壁を貫通する熱流の対称性を持つコンダクタンスが計算されます．

　二酸化炭素ガスの移動回路網による6日間の模擬測定データをグラフに示します．これには1階と2階それぞれへのガス流率と結果のガス濃度の変化が表されています．1階から2階への上昇の空気流率が下降のそれよりも大きいので，2階は1階のガス濃度の影響を受けています．ガス移動のシステム同定計算プログラム SPIDS-Gはグラフの変化量に5分間の移動平均を施してから両室間の双方向の空気流率と外気との空気流率を推定しました．
　以前の研究[99]では各室に電熱発熱流率4kWを正弦波形の谷から谷まで3日間与えました．これと同じ発熱総量の矩形波形では2日になります．実際には灯油暖房器を電子秤に載せて重量減少を計り発熱流率を推算します．伝熱のシステム同定は6日間の測定データから伝熱系のワンセットの係数を推定しますので，ガス移動系でも6日間の平均的な換気流率などを推定します．

　グラフに熱回路網モデルによる6日間の模擬測定値を表します．これらは各室での発生熱流，水平面全日射熱流，外気温，そして結果の室温の変化です．
　ガス濃度変化と違って室温変化は外気温の変化に大きく影響されることになります．また建物の外表面に吸収される日射量の合計から推察しますと，灯油暖房器をはるかにしのぐ大きな影響があると考えられます．従いまして日射熱取得係数の適切な同定がなされなければ，外壁の正確な熱損失係数の同定も難しいと思われます．　　
　熱系のシステム同定を行う計算プログラムSPIDS-Hに，これらの模擬測定データとガス移動系のシステム同定から求められた室間の空気流率を与えれば，壁を貫通する一般化熱コンダクタンスが計算されます．

　移動平均を1回だけ施すか2回施すかの違いによるシステム同定結果を示します．これらの棒グラフは，外皮全体の熱貫流のコンダクタンスUsと，2室合計の相当熱容量と，そして2室合計の日射熱取得係数，のシステム同定結果を比較したものです．ここにUsは様々な部位の外壁 j の熱貫流率Ujと面積Sjを乗じたUj･Sjの合計です．
　正解のUs値は定常の熱負荷計算により求めました．相当熱容量と日射熱取得係数は2012年の研究[99]のシステム同定結果を正解としました．1回の移動平均を用いて推定されたUs値は正解値に対する比率が0.92ですが，2回の移動平均を用いれば0.96となり１に近づいて良くなります．他の，相当熱容量も，日射熱取得係数も，同様に改善されます．
　正解値としたシステム同定では間欠的な正弦波形の励振を継続期間は3日間で与えました．しかし今回の矩形波の励振の継続期間は2日間です．そこで3日間に長くして，かつ2回の移動平均も施してシステム同定をすると，より正解値に近くなりました．

　システム同定結果により室温変化の予測計算モデルができます．一方，模擬測定結果としての室温変化もあります．良いシステム同定結果であれば予測計算室温は模擬測定室温に近くなります．比較したシステム同定の三条件 (a)，(b)，(c)は次のとおりです．(a)周期が3日間の正弦波形の励振を間欠的に与えて測定データには8時間の移動平均を施した場合．(b)一定値が2日間継続する矩形波励振を間欠的に与えて測定データに8時間の移動平均を施した場合．(c)一定値が2日間継続する矩形波励振を間欠的に与えて測定データには8時間の移動平均を2回施した場合．これら(a)，(b)，(c)の三条件の違いによる影響を2階の室温変化について比べました．三条件いずれの室温変化も模擬測定室温変化にとても近くなりました．　
　この模擬測定値生成の熱回路網モデルは63節点ありますが，システム同定モデルはたった2節点です．模擬測定値生成では，外壁への日射の吸熱も，日射の窓の透過も，太陽位置で変化します．しかしシステム同定で得られた予測計算モデルは変化しない 一定値の日射熱の取得係数を持つ単純なモデルです．それにも関わらず室温変化は良く一致しました．

　我々が建築の気密性能の評価方法と測定法関する研究を始めたきっかけは，1979年3月の米国のスリーマイル・アイランドの事故により，日本原子力研究所（東海）で始められた原発事故による放射性ガス拡散に対する家屋の放射性ガス防護効果の受託研究でした．これは家屋の隙間風の換気量が大きく関係します．
　これによりNETSやSPIDの開発も加速されました．第一世代の多数室換気測定システムも，この受託研究で開発されました．
　一方，サステナブルで健康的な建築志向では，壁体の高断熱と耐久性について内部結露が問題です．通気層の上下の狭いスリットを通す温度差換気により水蒸気が排出できます．壁内の水蒸気移動量は部材の湿気伝導よりは隙間風による割合が大きい場合が多いと思われます．
　一般に建物の気密性は送風機による加圧・減圧で測定することが多いのです．この従来のデータ分析法は，測定誤差に対するロバスト性と，信頼性評価が不十分ですので，改良する方法を2012年に Building and Environment 誌に発表しました[97]．
　近年では，相当隙間面積αAによる評価方法の問題から，隙間の数式はべき乗則ではなく二次式の可能性を検討しています．

　左の図は送風機による住宅の気密測定の様子と装置を示しています．日本工業規格のJIS A2201,2003 から引用しました．右上の写真は市販されている気密性能測定器です．隙間の数式モデルはISOもJISも本質は同じ べき乗則です．前者は空気流率を，後者は差圧を表す式を使います．どちらも回帰係数と指数を含みます．
　送風機の出力を制御して沢山の差圧と空気流率の組み合わせを測定します．これらに最小二乗法を適用することで回帰係数と指数を推定します．この方法は定常状態を仮定します．一方，室の圧力の時間変化の基礎式に基づいた非定常の測定法としては，ピストン装置で室空気に圧縮と減圧を与えて非定常の圧力の応答を用いる幾つかの方法も研究されています．
　本研究で扱うのは現状の測定データ分析法が不確かさと信頼性評価について不十分な問題と，べき乗則の式は単なるequation fittingに過ぎず物理学的な意味がない問題です．隙間の場合は回帰指数nが1から2の間になります．しかし指数nを2と固定して，回帰係数から得る相当隙間面積だけで気密性を評価するので，実現象との不整合があります．

　JISの気密性能試験方法の問題を考えます．伝統的な換気計算法では開口の圧力損失係数ζの代わりに幾何的な開口面積Aに流量係数αを乗じた実効開口面積αAをべき乗則の(4)式で用います．そして気密性能評価では隙間にも指数nは２に固定した(4)式が用いられます．一方，測定で回帰するのは(3)式の単純相当隙間面積sと指数nです．そしてJISの定義によれば差圧Δpが1mmAqつまり9.8Paの場合にsとαAは一致するようにαAを決めます．これは左下の図の2つの曲線の交点として示されます．相当隙間面積αAの単純相当隙間面積sに対する比率r_αAは(5)式で計算されます．比率r_αAはほぼ指数nの関数です．指数nが2の場合にr_αAは1ですが，指数nが1に近づくとr_αAは4と大きく違ってきます．
　また左下の図は実験建物の一例です[114]．実態の指数nが1.49の特性曲線と，指数を2に固定した特性曲線は大きく異なります．気密性能評価はC値とも呼ばれる相当隙間面積αAだけでなされますが，同じC値でも指数nにより隙間の空気流率はかなり違います．従って新たな隙間モデルと評価法を考える必要がありそうです．

　様々な隙間を平均的に代表する理想化した隙間の形状的なモデルを考えます．上の図に示す様に隙間を，長さはl，幅はw，深さはdの寸法で表現します．隙間のべき乗則の数式モデルを(8)式で表し最小二乗法の回帰係数Dnを定義します．ここにDnの添え字のnはべき乗則の指数nを意味します．単純相当隙間面積sは幾何的相当隙間面積と呼ぶwlより小さな面積になると考えられます．

　ここで新たに隙間の圧力損失を表す(9)式の二次式モデルを導入します．気流の通過途中の摩擦損失は空気流率qすなわち気流速に比例します．隙間風の出入り口での乱流による圧力損失は形状損失と呼ばれqの二乗すなわち運動エネルギーに比例します．ここで隙間幅wと深さdによる複合係数d/w2を相当隙間深さ率と定義します．この複合係数はナビエストークスの運動方程式を気流方向に空間積分して得られる数式の中に現れます．

　隙間の二次式モデルは(10)式で表されます．これはナビエストークスの方程式を隙間内の流れ方向に空間的な積分をして(10)式等が導かれることを本間宏 博士が述べています[116]．ただし様々な隙間の形状があるので(10)式の第一項のζと第2項の12の数値は普遍的ではありません．またDr. Mats Sandberg も彼の著書[49]で隙間モデルを述べています．
　一方，送風機による加圧・減圧試験で沢山の差圧と空気流率のセットから最小二乗法で式(9)の係数D1とD2が回帰されます．この(9)式と(10)式を見比べることで，複合係数w･lとd/w2を計算する(11)式と(12)式が記述できます．ただしζは隙間の形状で値が異なりますので1等を常に仮定するのが一つの方法だと思われます．係数12も同様の問題がありますが12が代表的と思われます．そしてw･lは相当隙間断面積，d/w2は相当隙間深さ率と呼ぶことができます．

　二種の隙間モデルの長短と測定値分析理論を比較表にしました．数式の外形は，べき乗則モデルは１つの項ですむので単純ですが経験的な数式であり指数のnには物理学的な根拠がありません．二次式モデルは２つの項になりますので見かけは複雑ですが理論的な理由があります．何れも測定データから二つの係数を最小二乗法で求めなければなりません．べき乗則モデルは対数尺度で行いますので推定精度が悪くなります．
　換気回路網計算プログラムNETSでは，送風機と流路の二本のP-Q特性曲線の交点として運転点を求めます．送風機のP-Q特性は三次方程式で，流路は二次式方程式で表して，カルダノの三次方程式の解法で素早く精確に解くことができます[11][20][24][63]．もし，べき乗則の流路の指数nが２ではない場合は，仮定した数十個の差圧Δpにより空気流率qを計算して，最小二乗法により近似二次式モデルをつくります．
　なお，2012年頃に，気密性測定データを分析する理論を考案しB&E誌に発表しました[97]．また表計算ソフトも開発してあります．なお最小二乗法の不確かさと信頼性の評価には測定不確かさ標準偏差が基本情報として必要です．そこで測定値が変化する場合でも移動平均による平滑化曲線からの偏差を統計処理する方法を考案しました[109]．

気密性能の評価方法の標準 JIS A2201の問題
◆相当隙間面積αAの評価法の問題
　べき乗則の式(i)に基づき，等価隙間面積αAと空気密度ρを用いて，圧力損失Δpと隙間空気流量qの関係式が記述できます．測定から多数のΔpとqの組を取得し，最小二乗法を使用して式(ii)の係数aと指数nが解かれます．式(i)をαAを計算する式に変形し，qに式(ii)を代入すると式(iii)が得られます．数式(ⅲ)の方がJISの数式よりも合理的ではないでしょうか？
　しかしJISでは式(i)の指数nを2に固定し，式(ii)を代入しているため，次式(iv)のようにΔpに応じてαAが変化します．そこで，Δpを9.8Paに固定した式(v)を用いますが，この曲線はΔpが0Paと9.8Paの2点を除いて回帰特性曲線とは大きく異なります（文献114参照）．
◆その他の問題
・減圧法と加圧法では建物外皮の収縮または膨張が起こり隙間は小さめにあるいは大きめに変化するので，両方を実施して違いが少ないことを確かめる必要があると思われます．
・べき乗則の指数nは1から2の値になるので数式の両辺の物理的な単位が整合しなくなる場合があると思われます．
・二次式モデルに比べて，べき乗則モデルでは摩擦損失を乱流損失に含めなければならないので，相当隙間面積は実際よりも過小評価されると思われます．

　各階に設置された灯油ストーブにより断続的に二酸化炭素ガスを発生させます．ガス発生スケジュールは隣り合う階が異なったガス濃度変化になるようにします．これは数日間にわたって続けられ各階のガス濃度の変化が測定されます．システム同定計算プログラムのSPIDSは，数日間の全測定期間のうちの数時間の部分的な期間に最小二乗法を施し，この期間はΔtずつ進行していきます．これらの期間においてゾーン間の空気流率が推定され，部分的な期間が移動するのに伴い空気流率の変化も現れます．これを移動最小二乗法と呼び次のスライドで図解されます．このようにして第j-階の外壁を通る隙間風流入率qj,oと流出率qo,jが求められます．また部分的な各期間で測定された室内外の圧力差Δpjの平均値も計算されます．数日間の測定期間内の沢山の部分的期間で推定されたqと測定されたΔpのセットに最小二乗法を適用して各階の相当隙間面積とべき乗指数が推定されます．風圧は変動するので差圧測定に悪影響を与えます．しかし長い期間の測定値の平均は正確と思われます．相当隙間面積とべき指数は階ごとに異なり沢山あります．良い最小二乗解を得るためには差圧Δpと空気流率qはなるべく長い期間の測定で沢山のセットを得る必要があります．

　建築の多数ゾーン系の換気測定のため，最小二乗法を基礎にして，測定期間での平均のゾーン間の複数の空気流率を推定する計算式を導き，さらにこの式をWoodburyのマトリックス・インバ―ション・レンマにより変形して逐次的にΔtの時間ステップ毎に空気流率等を推定する漸化式が導かれました（参考文献 13，26，99）．
　しかし，再帰的最小二乗法では妥当な結果は得られませんでした（参文17）．一方で，数日間の測定期間のうち数時間程度の期間に最小二乗法を適用し，この期間をΔtずつずらしていけば，妥当な結果が得られました（参文35）．
　例えば点々の曲線[A]は1分間隔で測定されたガス濃度を表します．データ[A]に数分間の移動平均を施し測定不確かさが平滑化された曲線[B]を得ます．曲線[B]からデータ[A]の偏差を全測定期間で統計処理して測定不確かさ標準偏差σが得られます（参文111）．これらは最小二乗法の推定そのものではなく，推定結果の信頼性評価に必要になります．
　全ての測定データに移動平均によるローパスフィルタを施し曲線[C]を得ます．移動平均期間は換気測定では数分間を，伝熱系では約8時間とします．もし矩形の加熱の場合はさらに二重に移動平均を施します（参文139）．
　そして移動最小二乗法の処理を行います．この期間の長さは各ゾーンでのガス発生が全ゾーンで一巡する時間とします．これで得られた換気流率の変化曲線は[D]で示されます．
　さらに励振の必要な大きさ（参文141）と最適な減衰期間（参文98）なども研究されました．

　空気流率の回路網計算モデルでは，各ゾーンでの流率収支を満たすように各底レベルでの静圧に関する非線形連立方程式が解かれます．各ゾーンの流率収支には，普遍的と思われている質量流率をとる計算プログラムもあるようです．しかし空調や換気の実務的な計算では空気流率は体積流率で扱われるので一貫性が損なわれます．また予測計算では空気移動系と熱移動系の連成計算を行います．この際に各ゾーンでの熱流率収支と空気流率収支の同時成立が考慮されれば，スライドに演繹する様に，体積流率をとる方が合理的なことが示されます．この考察において伝導や表面伝達などによる熱流は，これらの一般化熱コンダクタンスci,jが対称性のci,j=cj,iを持ちΣci,j=Σcj,iは自明なので，省けます．ただし空気は非圧縮性で流れの様子は瞬時に定常状態に達するという前提も必要です．熱と空気とガスの移動計算プログラムNETSにおける空気流率回路網モデルの解法では体積流率の収支を計算しています．